| |
Date: Wed, 7 Apr 1999 13:40:10 -0600 (CST)
Subject: Universal Area
Name: Karen
Who is asking: Student
Level: Middle
Question:
I need a formula for area that works for a square, a rectangle, a parallelogram, a trapezoid, and a triangle.
|
|
| |
Hi Karen,
An interesting problem. A square is a rectangle which is a parallelogram and so the formula for the area of the parallelogram gives the correct value for rectangle and square also. The area of a parallegram is the base times the height, that is, for the diagram at the right |AB| h.
|

|
|
| |
A trapezoid is a quadralateral with exactly two sides parallel. The area of a trapeziod is the average of the lengths of the parallel sides times the height. For the diagram at the right this is 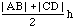
Notice that if you apply this expression to the parallelogram above then, since |AB| = |CD|, you get the area of the parallelogram.
|
 |
|
| |
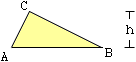
Now let us look at the triangle on the right. You might see this as a degenerate trapezoid with C = D so that the top is a point and |CD| = 0. If you use the expression for the area of a trapezoid with |CD| = 0 you get half the base times the height which is the area of the triangle.
|
 |
|
| |
Thanks for raising this question. None of the three of us had thought about it this way before. Th key seems to be that all of these figures are "trapeziods" of you think of a trapeziod to be a quadralateral with AT LEAST two sides parallel and you allow the degenerate situation that one of the parallel sides has zero length.
Cheers,
Jack, Chris and Harley
|
|


