Name: Katherine

Who is asking: Student
Level: Secondary

Question:
A circular garden has an a radius of 8m. Dig, the dog, is tied up to a fence that runs round the outside of the garden. Dig was able to dig up all the garden, apart from an area of 64 square metres, which he couldn't reach. How long was his lead?

Hi again Katherine
We have two solutions for you. One from Chris (know some calculus and work hard) and another from Harley (guess and be lucky).

If a is the length of the dog's leash then using calculus and polar coordinates the area of the portion of the garden that Dig can't reach is

Finding a value of a that makes this expression equal to 64 looks impossible, so lets try the other approach.

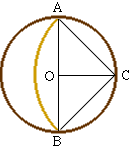
The garden has an area of 64 square meters and is approximately 3 so I drew a diagram and tried to estimate the length of the leash so that approximately one third of the area (64 square meters) would be beyond Dig's reach. My estimate lead me to guess that the configuration was as in the diagram, that is so that the line joining A and B goes through the center O of the circle that bounds the garden.
   Since |AO|=|OC|=8, the theorem of Pythagoras gives |CA|=8. The portion of that garden that Dig can reach is then the sector CAB plus the two "caps" above CA and BC. The sector CAB has area

The area of the two "caps" is the area of the semicircle BCA minus the area of the triangle BCA, that is

Thus the area that Dig can dig is 64  - 64. Since the area of the entire garden is 64 , the arera that he can't reach is 64 square meters.So my guess was correct.
   Now you can go back to the expression that Chris obtained and substitute a = 8 to verify that this gives an area of 64 square meters also.