Who is asking: Student
Level: Secondary

Question:
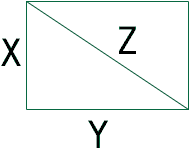
The sides of a rectangle increase in such a way that dz/dt=1 and dx/dt=3*dy/dt. At the instant when x=4 and y=3, what is the value of dx/dt? (there is a picture of a rectangle with sides x and y, and they are connected by z, which cuts the rectangle in half)

Hi Tammy

I assume that "z" is a diagonal of the rectangle.    In these related rates problems there are always some quantities which have rates of change that you either know or are interested in finding. In this problem the quantities are x, y, and z. Perhaps you should write them x(t), y(t), and z(t) as they are all functions of time, t.    The first step is to find, if possible, an expression that relates these quantities. In your problem x, y, and z are the sides of a right angled triangle so an expression that relates the three quantities is X2 + Y2 = Z2    Now, using implicit differentiation, differentiate both sides with respect to t. This will give you an expression relating dx/dt, dy/dt and dz/dt. Use the facts that you know at the specific time of interest, dz/dt=1, dx/dt=3*dy/dt, x=4 and y=3 to find dx/dt at this time.

Cheers
Harley