Dear MathCentral,

I'm no schoolkid, but I liked your answers about triangles. You might enjoy a quick look at this, the kids may too.

I was working on a Voronoi dual where I had to calculate the areas of very many triangles expressed as vertex coordinates, so I derived the following very direct formula:

A = abs((x1-x2)*(y1-y3)-(y1-y2)*(x1-x3)) for triangle (x1,y1)(x2,y2)(x3,y3)

I've never seen this in a textbook. Is it original? I doubt it, the proof is only a few lines long.

Regardless, it may be fun for the kids, even if it's not on the curriculum.

Mark

Hi Mark,

Yes it is an old formula. It is implicit in most linear algebra books and vectors books. It is really the cross product of the vectors (x₁-x₃, y₁-y₃) and (x₂-x₃, y₂-y₃) along the two edges of the triangle out of the vertex 3.

More generally, it is connected to the area of a triangle as a determinant of the three points in affine coodinates:

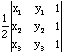
I am pretty sure that goes back to Mobius (1820's or 30's) who developed these affine coordinates. As such, it generalizes to a 4x4 determinant for the volume of a tetrahedron (and 2x2 determinant for the length of a line segment!). In general, volumes (length area ... ) and determinants are very closely related in all dimensions (even the fourth dimension and higher).

Walter Whiteley
York University