Name: Lars-Åke
Who is asking: Student

Question:
My problem is to get an equation for the depth of the oil in a gastank formed like a cylinder. The cylinder is in a horizontal position and by a stick you will be able to get the depth of the oil in the tank. All I need is an exmaple which I can build on. By this equation you will be able to get the volume of the oil if you know the depth.

Many Thanks

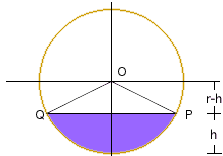
Hi I have drawn the diagram with the height of the oil in the tank, h, less than the radius of the cylinder,r. If h is greater than r the argument is similar. The volume of the oil in the tank is the area of the oil cross section (shaded blue) times the length of the tank.The area of the oil cross section is the area of the sector OQP minus the area of the triangle OQP.    If the angle POQ is theta then the area of the sector is (1/2)r2theta. From the diagram cos(theta/2) = (r-h)/r and thus theta is the twice the angle whose cosine is (r-h)/r.    To find the area of the triangle OQP solve the equation of the circle, x2 + y2 = r2, with the equation of the line through P and Q, y = -(r-h), to find that the first coordinate of P is , then the area of the triangle is (r-h)x0

Cheers
Harley