I am a middle school teacher who is looking for a precise explanation of why zero raised to the zero power is undefined. I am hoping to get an explanation using something other than the fact that diividing by zero is undefined.
Thank you!!
Hi,
We have had this question before and answered it but I want to expand on the answer. I want to start with a0 where a is a positive number. To see what this "should be" my technique will be to calculate ab for values of b that get close to zero. One way to do this is to calculate
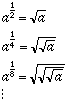
Try it. Choose some positive number and use your calculator to take successive square roots. The sequence of numbers you get approaches 1. This is the type of reasoning that convinced mathematicians to use the convention that a0 = 1 if a is positive.
Trying this same technique with ab leads to confusion. If you calculate 0b for values of b that get close to zero you always get 0b = 0 which might lead you to suggest that 00 should be 0. However if you calculate a0 with a positive and close to zero you always get a0 = 1 which might lead you to suggest that 00 should be 1. If you start with a and b both not zero but getting close to zero you can produce an argument to say that 00 should be anything you want. For example if
both of which get close to zero as n increases then you get
| n | a | b | ab |
|---|---|---|---|
| 1. | 1. | 0.25 | 0.25 |
| 2. | 0.5 | 0.125 | 0.353553 |
| 3. | 0.333333 | 0.0625 | 0.39685 |
| 4. | 0.25 | 0.03125 | 0.420448 |
| 5. | 0.2 | 0.015625 | 0.435275 |
| 6. | 0.166667 | 0.0078125 | 0.445449 |
| 7. | 0.142857 | 0.00390625 | 0.452862 |
| 8. | 0.125 | 0.00195312 | 0.458502 |
| 9. | 0.111111 | 0.000976562 | 0.462937 |
| 10. | 0.1 | 0.000488281 | 0.466516 |
The larger n, the closer ab gets to 1/2 so maybe 00 should be 1/2.
It is this ambiguity that had led mathematicians to use the convention that 00 is undefined.
Cheers,
Penny