Subject: Vector problem

Hi, here's the problem.

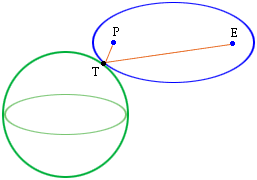
Given two points P,E and a sphere. Find a point on the sphere, T, so that a line from P that bounces off the sphere at T goes through point E.

My names, Mark I work in Computer Graphics.

The reflection phenomena that you describe is a property of an ellipe. Geometrically you have a sphere, two points P and E and you want to construct an ellipse with foci P and E that is tangent to the sphere. The point of tangency is the point T. (Actually there are two such ellipses, and hence two T's, one on the other side of the sphere.) Algebrically this problem is intractable.

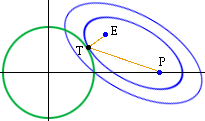
The problem is inherently planar so consider the plane containing the center of the shpere and the two points P and E. Translate the circle of intersection of the sphere and this plane so that its center is at the origin of the plane, rotate the diagram to put P on the X-axis and change the scale so that the radius of the sphere is 1. Of all the ellipses with P and E as foci and that intersect the circle at some point T, you want to find T so that |ET| + |TP| is a minimum.

Since the circle has radius 1, if t is the angle in the diagram below then the coordinates of T are (cos t, sin t).

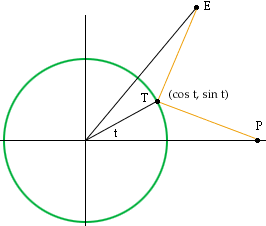
Write an expression for f(t) = |ET| + |TP|. (Remember that these are not the original E and P.) This is the quantity you need to minimize. I suggest now that you use some calculus. Differentiate f(t) and solve f'(t) = 0. This is still intractable but f'(t) is a function of one variable and you can use some iterative technique, for example Newton's method, to find an approximate solution to f'(x) = 0. Since you know that t is between 0 and the angle formed by the X-axis and the line joining E to the center of the circle, you can easily find an appropriate starting value for the iteration.