My name is Alan.
Grade: 12 (AP Calculus BC)
Who: Student

I have 2 questions that are very new to me, they were included on a quiz and the material was never covered. Our teacher never explained the purpose and detailed explanation of how to solve the problem. Could you help? Thanks.

Question 1:
A ball is falling 30 feet from a light that is 50 feet high. After 1 sec. How fast is the shadow of the ball moving towards the light post. Note that a ball moves according to the formula S=16t^2

Question 2:
How many trapezoids must one use in order for the error to be less than 10^-8 if we want to find the area under the curve Y=1/X from 1 to 2. Find the exact area, Graph the function and use the trap rule for the "N" that you found.

I would appreciate a succinct explanation with minor work, not something real detailed or something you have to labor over. I just would like to see how to conceptualize the problem by setting it up and the answer I should get. Thank you for your help.

Hi Alan,

Question 1

In the diagram below L is the light, B is the ball, P is the position of the shadow, s is the height of the ball from the ground ans x is the distance from the base of the light post to the sahdow.

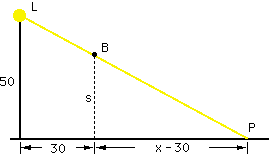
By similar triangles

or

x and s are both functions of time, t in seconds, so differentiating with respect to t gives,

Since s = 16 t², ds/dt = 32 t and thus when t = 1 sec ds/dt = 32 feet, s = 50 - 16 = 34 feet and, using the similar triangles expression x = 1500/16 feet. Substituting into the equations above gives dx/dt = -1500/8 = 187.5 feet/sec.

Question 2

The expression for approximating an integral with trapezoids is

where and

The error E satisfies

where for all x between a and b.

For problem function f"(x) = 2/x³ a = 1 and b = 2 and hence |f"(x)| is bounded by 2 on [1,2] so you can take K = 2. Let E = 10^-8 and solve for n. Make sure that you round up.

I hope this helps,
Harley