Date: Mon, 07 Aug 2000 18:08:31 -0500 Subject: PreCal absolute value, degree measure, angular speed

I am a student in the 12th grade doing an AP Calculus assignment with Precalculus review. I have some questions on some things I don't remember. Your help would be greatly appreciated as soon as possible.

1. Use absolute values to define the interval or pair of intervals on the real line.

   <--|---|---]---|---|---|---[---|---|--> 
     18  19  20  21  22  23  24  25  26   
   

   It's something like this: |x| <= 20 or |x| >= 24 But I don't think that is right because it should be one formula. If the 20 and everything in front of it were negative I could do: |x-2| >= 22 I can't think of anything that would work for this situation. Can you help?
    
   

2. I have another question about expressing angles in degree measure. Is there a certain way to work this out for the angle measuring 0.438 or can it only be done on a calculator?
    
   
3. A car is moving at the rate of 50 miles per hour, and the diameter of its wheels is 2.5 feet.
   a) Find the number of revolutions per minute that the wheels are rotating.
   b) Find the angular speed of the wheels in radians per minute.

   I have some formulas for this but I'm not sure how to use them especially for part
   b). Angular velocity, where w= change in an angle with respect to time: w= (radian/time) Linear velocity, where v= movement along an arc with respect to time: v= rw (distance/time)

   For a) I used: (1.25ft is the radian)

   w= (50mi/1hr) (1/1.25ft) (5280ft/1mi) (1hr/60min) (1revolution/2) w=560.235 rev/min

   Is this right? This formula does not work for part b). Do you know what I should do? Thanks!

Angela

1. It helps to think of absolute value as distance, for example |4-7| is the distance between 4 and 7. For your problem consider some point x on the line. Then x is in the region you want if its distance from 22 is at least 2. That is x is in the set you want if |x - 22| >= 2.
    
   

2. To find the measure of an angle in radians, construct a circle of radius 1 with center at the vertex. The radian measure is the length of the arc on the circle. Thus if the degree measure of the angle is 180o then the arc is half the circle circumference, and thus the radian measure of the angle is 2 pi/pi = pi. That is pi radians = 180 degrees or 1 radian = 180/pi degrees. Therefore 0.438 radians = (180/pi) 0.438 degrees.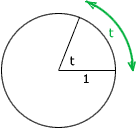

   
    
   
3. I find it easier to work with the units than to memorize formulas.

   In part a) you are looking for an answer in revolutions/minute. The diameter of the wheel is 2.5 feet so the circumference is pi times 2.5 feet or 7.8540 feet. Hence one revolution is 7.8540 feet and thus there are 1/7.8540 = 0.1273 revolutions/foot.

   The car is travelling at 50 miles per hour, that is 50*5280 = 26 4000 feet/hour. Thus the wheel is moving at

   0.1273*26 4000 (revolutions/foot)(feet/hour)
   = 33613.4 revolutions/hour.

   Since there are 60 minutes per hour this is

   33613.4(1/60) (revolutions/hour)(hours/minute)
   =560.22 revolutions/minute.

   Again, there are 2 pi radians in one revolution so the angular velocity is

   560.22 (2 pi)/1 (revolutions/minute)(radians/revolution)
   = 3520 radians/minute.