Subject: PreCal ques: trig

I have some PreCal questions. I am a student at the secondary level. I would be very grateful for your help.

Solve the equation for theta (0 <= theta < 2pi).

1. tan²(theta) = 3 I know sec²(theta) -1 = tan²(theta)
    
   
2. sin(theta) = cos(theta) How would I go about solving these equations?
    
   

also:

3. In traveling across flat land, you notice a mountain directly in front of you. Its angle of elevation (to the peak) is 3.5 degrees. After you drive 13 miles closer to the mountain, the angle of elevation is 9 degrees. Approximate the height of the mountain.

   I solved it this way, but the answer doesn't seem right. (sin5.5 degrees)/(13) = (sin3.5 degrees)/(b) ; b is the side opposite the angle 3.5 8.28 mi = b (sin90 degrees)/(8.28) = (sin9 degrees)/(x) ; x is the height of the mountain 1.3 mi = x

4. The model for the height "h" of a Ferris wheel car is h = 51 + 50sin[(8pi)t] where "t" is measured in minutes. (The Ferris wheel has a radius of 50 ft.) This model yields a height of 51 feet when t = 0 . Alter the model so that the height of the car is 1ft when t = 0.

   I don't know what to do for this. I'm lost.

Thank you for your help,
Angela

I am a very strong believer in drawing diagrams. In a math problem, if it makes any sense at all to do so, draw a diagram.

1. From what you have said sec2(theta) = 4. Also since (0 ≤ theta < 2pi), sec(theta) = 2. Now draw a right triangle with sec(theta) = 2. What is the length of the third side? do you recognize this triangle? What is theta?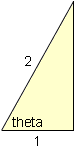

   
    
   
2. Again, draw a diagram. This time draw a right triangle and label its sides a, b and the hypotenuse c and label one angle as theta. Write sin(theta) and cos(theta) in terms of a, b and c. Set these expressions equal. What does this say about a and b? What is theta?
    
   

3. Again a diagram is appropriate. Here h is the height of the mountain in miles. From the diagram tan(3.5o) = h/(13 + x) and tan(9o) = h/x. Solve the second equation for x, substitute in the first equation and solve for h.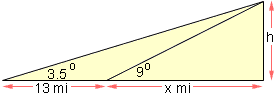

   
    
   
4. Here I don't see that a diagram helps. I think of two people building a model for the height of the Ferris Wheel. One of them uses the letter t to designate time and starts his clock when the height is 51 feet. He gets the model h = 51 + 50sin[(8pi)t] The second person uses the letter t^* to designate time and starts her clock when the height is 1 foot. In the first model h = 1 foot when sin[(8pi)t] = -1, that is when (8pi)t = (3/2)pi or t = 3/16 minutes. Hence the first person's clock is always 3/16 minutes ahead of the second person's clock, that is t = t^* + 3/16. The second person then just has to substitute this value for t into the first model to et her model.