Subject: help with matrices
Suppose that taxis pick up and deliver passengers in Chicago, which is divided into three zones. Records kept by the drivers show that of the passengers picked up in Zone 1, 50% are taken to a destination in Zone 1, 40% to Zone 2, and 10% to Zone 3. OF the passengers picked up in Zone 2, 40% go to Zone 1, 30% to Zone 2, and 30% to Zone 3. Of the passengers picked up in Zone 3, 20% go to Zone 1, 60% to Zone 2 and 20% to Zone 3. Suppose that at the beginning of the day, 600 of the taxis are in Zone 1, 100 in Zone 2, and 300 in Zone 3. What is the distribution of taxis in the various zones after all have had two riders?
How do you set up a matrix for this problem? I don't understand how you are supposed to go about solving this.
Hi,Suppose that Z1 is the number of passengers in Zone 1, Z2 the number in Zone 2 and Z3 the number in Zone 3. After they have all had one taxi ride these numbers have changed. Let NZ1 be the new number in Zone 1 after they have all had one ride, NZ2 the new number in Zone 2 and NZ3 the new number in Zone 3. The description on the process in the problem tells you now to find the new Z's from the old Z's. For example
That is 50% of the passengers who start in Zone 1 remain in Zone 1, 40% of the passengers who start in Zone 2 go to Zone 1 and 20% of the passengers who start in Zone 3 go to Zone 1.
Likewise
and
In matriz form these equations can be written
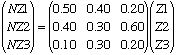
Harley