Who is asking: Teacher
Level: Elementary
Question:
I am having problems finding examples of problems that require "Working Backwards" used as a strategy for solving. We are required to give a presentation on Monday, October 25, 1999 in our school districts math class. We are trying to become better problem solvers and how to teach problem solving in the elementary classroom. Help! I can't find anything in my web searches. I am mathematically challenged so I am also very terrified of any math above 5th grade level. Thank you for your help.
Linda Bach
Hi Linda,
Here is one problem that you can easily modify to include fractions or percentages if those are topics you are dealing with.
You can introduce another step if you wish.
If there is only one stair, then there is only one way to climb this stair.
If there are two stairs, then there are two ways to climb the stairs, by taking two steps or one big step (covering two stairs)
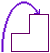
If there are three stairs, then the rabbit can take 3 small steps take a big step and then a small one or a small step followed by a big step.
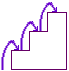
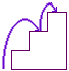
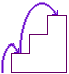
If there are four stairs, then the rabbit can climb the stairs in
four small steps
two small steps and a large step
one small step, then a large, then a small
one large step, then two small steps
or two large steps
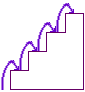
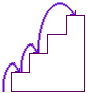
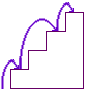
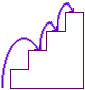
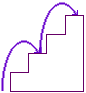
Thus we have
| Number of steps | 1 | 2 | 3 | 4 |
| Number of ways to climb the steps | 1 | 2 | 3 | 5 |
Now look at the four step problem with a "looking backwards" strategy. Suppose the rabbit has just arrived at the top. It got there either by being on the third step and hopping up one step or it was on the second step and got there by hopping up two steps.
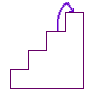
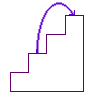
From what we did before there are 3 ways to get to step three and 2 ways to get to step two. Thus, there are 3 + 2 = 5 ways to get to step four.
Similarly for a 5 step flight of stairs there are 5 ways to get to step four and 3 ways to get to step three and thus there are 5 + 3 = 8 ways to get to step five.
So now we have
| Number of steps | 1 | 2 | 3 | 4 | 5 |
| Number of ways to climb the steps | 1 | 2 | 3 | 5 | 8 |
The pattern in the bottom row of the table should now be clear. Each number in this row (after the first two) is the sum of the two previous numbers. Thus it is easy to continue this row.
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10,944,...
Hence there are 89 nine ways for the rabbit to climb ten stairs (and 10,944 ways for it to climb 20 stairs!)
I hope this helps,
Cheers,
Penny