Hi,

My name is Chris Baranski and I have a math problem. I am in grade 10 but I think the question is far beyond grade 10 level. My dad got this problem while attending university and since I enjoy math he gave me this problem which he has never found an answer to. Here it is:

There is a well and in the well there are 2 sticks one is 2 meters long the other is 3 meters long and they are opposite to each other. They are leaning against the wall of the well. The place where they touch is 1 meter of the bottom of the well. How wide is the well? I have worked on this question with  friend for a very long time and come up with nothing I would like to know
  1. if there is any other way to figure this out other then trial and error and
  2. how do you do it

Hi Chris,

I don't have a nice way to solve this problem. The solution given here rersults in a quartic which I then solve by approximation.

In the diagram below |AC| = 3 and |BD| = 2 and |BC| = x is the width of the well.

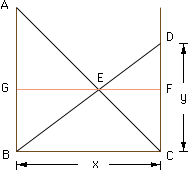
It is more convienent to work with y = |CD|, but Pythagoras' Theorem for triangle DBC gives

x2 = 4 - y2.

Likewise Pythagoras' Theorem for triangle ABC gives
|AB|2 = 9 - x2.

Thus,

|AB|2 = 9 - x2 = 9 - (4 - y2) = 5 + y2

Triangles DEC and ABE are similar anf thus,

Also triangles DEF and BEG are similar and hence

Hence,

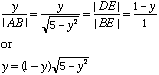
Squaring both sides yields,

y4 -2y3 + 5(y-1)2 = 0

At this point I used some graphic software to plot the graph of f(y) = y4 -2y3 + 5(y-1)2 to see where it crosses the x-axis. It does so twice at y = 0.7 and y = 1.58. Since y must be at least 1 the correct solution is y = 1.58 and since x2 + y2 = 4, x = 1.23.

Cheers,
Chris

Go to Math Central