Hi there - please help!

The question is a Year 10 level and I am a student trying to get it done for homework/exam revision.

This is it:

a semi-circle and an isosceles triangle ABC have the same base AB and the same area. The equal angles in the triangle are BAC and CAB. I have to find the value of each of these angles.

There is no more information given. How do I do this !!!!???

With so many thanks for your help, please send solution (am I being hopeful?) to

Ever grateful - Ben

I think that the angles that are equal are ABC and CAB.

In the diagram below let CP be the bisector of the angle BCA. Thus triangles CAP and CPB are congruent and angle CPB is a right angle. Since |AP| =|PB|, P be the midpoint of the line segment and r = |AP| is the radius of the circle.

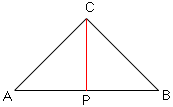
The area of the semicircle is 1/2 pi r² and the area of the triangle is 1/2 |AB| |CP| = r |CP|. Thus

The angle whose tangent is pi/2 measures about 1.00388 radians, which is about 57.52 degrees. Be careful not to confuse tangent of the angle pi/2 (which is the undefined quantity 1/0) with the angle whose tangent is the number pi/2 (which is just some angle in the first quasdrant).