Question:
One corner of a page of width a is folded over and just reaches the opposite side. Express L, the length of the crease, in terms of x and a.

I can't get the picture to copy to this form so I guess I will have to try and describe the picture the best that I can. The top right hand corner is folded to the left side, almost half way down. The width of the paper is a ( the width of the bottom part which is not folded.) The creased side is L and the part shorter part of the folded area is x (the part that would have been the top right of the original piece.)

I hope that this is good enough for you to understand.

In the diagram below the point P is folded to the point S leaving the "crease" QT of length L. PS is the line segment joing P and S.

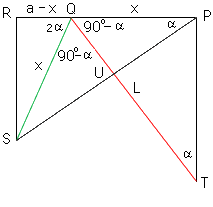
Triangles PQU and QSU are congruent and thus angle QUP = angle SUQ. Since their sum is 180^o they are each 90^o angles. If angle QPU = angle USQ = a then angle PQU =angle UQS = 90^o - a. Therefore angle SQR = 2a.

Using triangle SQR we see that

Using the fact that

we see that

Also from triangle PQT

Thus

Cheers,
Chris