trigonometric equation, extending solution. 2cos -5cos-3 = 0 for between -360 and 720 degree

When I factor[ 2cos (square) - 5cos -3], I get (2cos + 1)(cos - 3). 2cos + 1 = 0, 2cos = -1, cos = -0.5,. Using inv cos on calculator, I get 120 degree related angle.

When I graph I get two values, between 90 and 180 degree and between 180 and 270 degrees. How do I find those two values. How do use 120 degree in relation with the x axis. Maybe my factoting is wrong.

thank you in advance
my name is Pierre Iam taking a corespondence course.

Hi Pierre,

Your factoring is fine. The difficulty arises in trying to solve cos x = -1/2. I would quickly sketch a graph of one cycle of y = cos x, for x from 0^o to 360^o.

Notice that the graph crosses the x-axis at 90^o and 270^o. If you draw horizontal lines ay y = 1/2 and y = -1/2 you see that there are two values of x, at Q and R, where cos x = -1/2 and two values of x, at P and S, where cos x = 1/2.

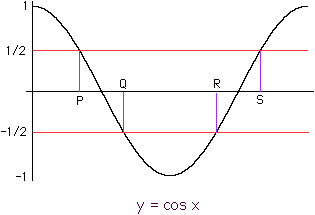
The key to finding Q and R is to first find P. Either by using the inverse cosine on your calculator or by using the "30-60-90" triangle you can find that P = 60^o. Now from the symetry of the diagram P is 30^o to the left of the intersection point at 90^o so Q is 30^o to the right of 90^o. Thus Q is 90^o + 30^o = 120^o. For the other pair of points R is 30^o to the left of 270^o and S is 30^o to the right. Thus R is 270^o - 30^o = 240^o and S is 270^o + 30^o = 300^o. Hence cos x = -1/2 at 120^o and at 240^o.
   These are only the values of x between 0^o and 360^o. You can add or subtract integer multiples of 360^o and get many more solutions.

Cheers,
Penny