Everybody seems to understand that "3 times 5" counts the objects in three sets, each of which contains five objects. Of course, "5 times 3" is quite different from "3 times 5" (even though the total count is still 15) since 5 x 3 counts five sets, each of which contain three objects. It is quite easy to visualize why 3 x 5 = 5 x 3:

Most people understand that negative numbers are useful for number scales such as temperature and years BC and AD. Negatives also have a simple meaning when keeping track of money. If a person owes money he can be thought to have a negative amount. If five people each owe $3, it is easy to understand that a total of $15 is owed, and the natural way to write this fact is 5 x (-3) = -15. But what is the meaning of (-3) x 5? Multiplication by a negative number has no concrete meaning of the form "take minus three sets, each of which contains five objects".

This lack of an obvious meaning might be the reason why it took so long for negative numbers to be accepted by the mathematical community. Although their usefulness had been recognized for thousands of years, negative numbers formerly had a different status from our familiar counting numbers. They were thought of as "fictitious," and were avoided in published documents until the 1800s, at which time people found them so useful they just started to use them. By the mid 1800s they were well understood and mathematicians seem to have gotten accustomed to living with them: at the start of the century the majority of mathematicians avoided them, but by 1850 or so the majority accepted them. What happened was that mathematics was becoming more abstract. If objects behaved as numbers should behave, then why not treat them as numbers? Why not declare that (-3) x 5 = 5 x (-3)? The process simply called for addition of a negative number to work like subtraction:

Return to the concept of money, where negative numbers make sense; here subtraction such as

means that if you take 3 dollars from a pile of 5 then 2 dollars remain in the pile. Using negative numbers this same idea can be written

so if your income is 5 and the amount owing is 3, then your balance is 2. For this system to work, one needs a complete set of rules like, for example, the rule that -(-3) behaves like 3. It doesn't have to have any concrete meaning; it just has to make subtraction work like adding a negative number. Of course the rule is not arbitrary – it must be justified by some interpretation that everybody finds reasonable.

One such interpretation considers the collection of horizontal arrows that have unit length. An arrow is assigned the number 1 if it points to the right and has a length of 1 unit; an arrow is assigned -1 if it has unit length but points left. Multiplication by 2 of a right arrow that is 3 units long is easily pictured as a right arrow of length 6:

We now extend this model by saying that multiplication by —1 means "reverse the direction of the arrow." Thus

, and we see that — 3 can be thought of as

or as

.

The system is completely consistent – it makes no difference if one reverses direction before or after the multiplication:

while also

.

In this model it is easily seen that — (—1) = 1 (since when you reverse directions twice you are facing the original direction). Likewise,

.

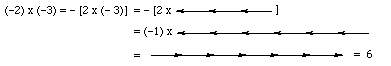After some practice a person quickly realizes that he should replace something like — (— (— (— 6))) by 6. Unhappily, even after lots of practice many students still find that combining adding, subtracting, and multiplying in the same problem causes difficulties: — (5 — 3) = —5 + 3 = —2. That probably means that they haven't practiced enough. The general rule is that one should practice using a new concept until becoming so used to it that it all seems to be obvious.