Subject: Cones

I am not a student, I am trying to solve a business problem. The question. If I want to put a lining in a chute that is cone shaped, how do I calculate the size steel plate I need to do that. The cone is 10' in diameter at the top and has a 20" hole at the bottom. The total height of the chute is 8'.

I would very much appreciate your help on this. Jim Campbell

In the diagram below the radius at the top of the cone is 5 feet and the radius of the hole is 10 inches or 5/6 feet. Since triangles PQV and SRV are similar 5/h = (5/6)/(h-8). Solving gives h = 9.6 feet. Now using the theorem of Pythagoras on triangle PQV we can find the slant height L. L² = 9.6² + 5² and hence L = 10.8240 feet.

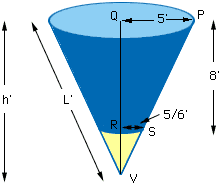
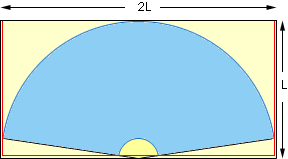
If you now imagine slicing hertically through the cone and rolling it out you get the diagram below. (Here I have rolled out the entire cone including the hole.) Since the radius of the large arc below is the slant height L, the lining can be cut from a steel plate 2L by L, that is 21.65 feet by 10.82 feet. You don't need a plate of quite this size as you can see by the diagram. You just need a plate of the size outlined in red. The minimum size plate is of length 21.5 feet and width 10.25 feet.

I hope this helps,
Harley