Solve for x: The absolute value of x-1 is less than or equal to the absolute value of x-2

Hi Austin,

To do this you need to think about the meaning of absolute value.

|y| = y	if y 0
|y| = -y	if y < 0

That is if y < 0 then change its sign by multiplying by -1.
Thus

|x - 1| = x - 1	if x - 1 0 (that is x 1)
|x - 1| = -(x - 1)	if x - 1 < 0 (that is x < 1)

and

|x - 2| = x - 2	if x - 2 0 (that is x 2)
|x - 2| = -(x - 2)	if x - 2 < 0 (that is x < 2)

Hence you need to divide the line into three pieces, by cutting it at x = 1 and x = 2, and solve the equation in each piece.

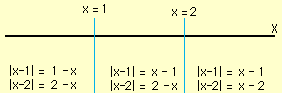
• If x < 1 then |x - 1| 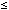|x - 2| if and only if 1 - x  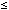2 - x, that is if and only if 1  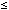2. But 1 is less than 2 so |x - 1|  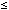|x - 2| is true for all x < 1.

• If 1 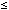x < 2 then |x - 1| 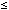|x - 2| if and only if x - 1  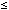2 - x, that is if and only if x  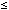3/2.

• If 2 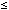x then |x - 1| 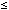|x - 2| if and only if x - 1  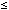x - 2, that is if and only if -1  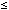-2. Since -1 is not less than or equal to -2, |x - 1|  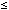|x - 2| is false for all x satisfying 2  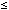x.

Thus |x - 1| |x - 2| if and only if x  3/2.

Cheers,
Harley