This is a problem inÊreal life, but I'm just trying to find the solution for my own satisfaction although it has practical application.

We start a Line that goes up 1 unit, then it goes to the Right for 5 units long, and then goes down 1 unit which is the end point. If we draw a circle that is tangent to both ends as well as the mid-point of the horizontal line: How do we find the radius of the arc; in Mathematics, with only this information?

So, if anyone knowsÊhow to get the answer. I willÊreallyÊappreciate the information.

THANKS.

The situation the way you describe it is impossible. At any point P on a circle the tangent line at P is perpendicular to the line joining P to the center ( a radius). For your situation that would mean that the center is at C in the diagram which it clearly can't be.

If we draw a circle is only required to pass through both ends as well as the mid-point of the horizontal line then there is a solution that can be described by putting a coordinate system on the plane.

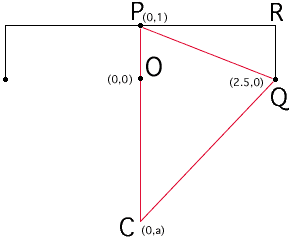
In the diagram C, the center of the circle, has coordinates (0,a). Let r be the radius of the circle then r = |CP| = a + 1. CQ is also a radius of the circle and triangle CQO is a right triangle. Thus by the theorem of Pythagoras,

Thus

a² + 2 a + 1 = 2.5² + a²
2 a + 2 = 2.5² + 1
2(a + 1) = 6.25 + 1
r = a + 1 = 7.25/2 = 3 5/8

Cheers,
Chris