My name is Tara Doucet
I am a university student taking a level 1 calculus class

1. The height of a cylinder with a radius of 4 cm is increasing at rate of 2 cm per minute. Find the rate of change of the volume of the cylinder with respect to time when the height is 10 cm.

2. A 24 cm piece of string is cut in two pieces. One piece is used to form a circle and the other to form a square. How should the string be cut so the sum of the areas is a maximum?

Hope you can help

1. In these so called "related rates" problems you need to find a relationship between the quantity whose rate of change you want to find (here the volume) and the quantity or quantities whose rates of change you know (here the height of the cylinder). The relationship between these quantities in the volume of a cylinder

   V = pi r² h

   For your problem the radius is a constant, 4 cm and thus

   V = pi 4² h = 16 pi h

   V and h both vary with time so you can differentiate both sides with respect to time, t, to get

   dV/dt = 16 pi dh/dt

   Now use the fact that dh/dt = 2 cm per min to find dV/dt.

2. This is one of my favourite max-min problems.

   When you cut the string let one piece be of length x and then the other piece will be of length 24 - x.

   

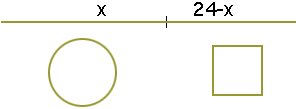
   Use the piece of length 24 - x to form the square, so each side of the square will have length (24 - x)/4 and its area will be

   

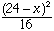
   Use the piece of length x to form the circle, so the circle will have circumference x. Thus x = 2 pi r, that is r = x/(2 pi). Hence the area of the circle is

   

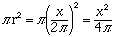
   Thus the sum of the areas is

   

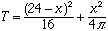
   Now maximize the function T. Make sure that you check to see that the answer you get is actually a maximum