Problem:
A truck full of cans of blue and white paint flips over on the road. There are dots of blue and white paint everywhere. Prove that two dots of the same color paint are exactly pi feet apart.

Thank you.
Lauren Emerson

Let P be a point in the plane and suppose that it is white. (If it is blue the argument is still valid, just interchange white and blue.) Construct a circle of radius pi and center P. Let Q be some point on the circumference of the circle. If Q is white then P and Q are the points required. If Q is blue construct a circle of radius pi and center Q. Let R be one of the two points where the circles intersect.

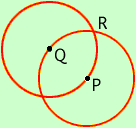
If R is white then P and R are the desired points. If R is blue then Q and R arre the desired points.

An interesting feature of this problem is that it is true for any number, not just pi. What I mean is that if A is any positive number then there are two dots of the same color paint are exactly A feet apart.