Subject: Geometry

Name: Ebony Indalecio Who is asking: Student Level: Secondary

Question: I need to prove the theroem: Tangents to a circle at the end points of a diameter are parallel.

There are a number of ways to prove these are parallel - depending on what other 'theorems' about parallel lines you have access to.

E.g. If you take the diameter and extend it as a line, you find that all the angles of intersection with the tangents are 90 degrees. In particular, this means that the angles labeled alpha are equal.

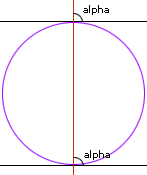
In some systems, that is enough to guarantee they are parallel.

Here is a nice proof that does not require much more than the idea that 'parallel' means the lines do not intersect.

Assume the two tangents interstect at some point P. Perhaps on the right of the diagram.

Now do a half turn of the entire figure around the center of the circle. The diamater goes to the diameter. The circle goes to the circle. The 'top' tangent goes to the bottom tangent.

The figure is, in fact, the same as it started out. However, any intersection to the 'right' would now be to the 'left'. There would not be just one point of intersection but two. Two distinct lines CANNOT have two points of intersection. (Any two points define a UNIQUE line.) Therefore, we were wrong to assume there was a point of intersection.

The lines do not interesct - they are parallel.

Cheers,
Walter