Question:
Here's a calc question that is probably a lot easier than I am making it. If you have a legendary "baseball problem" for the related rates section of Calc I, and you are given that the runner is running from 2nd to 3rd base at a given rate, and the umpire is standing at home plate, and you are given the distance between the bases on the field, how do you find the rate of change of the angle between the third base line (from the point of the umpire) and the runner? Here is a sample prob: Runner is moving from 2nd to 3rd base at a rate of 24 feet per second. Distance between the bases is 90 feet. What is the rate of change for the angle (theta, as described previously) when the runner is 30 feet from 3rd base? Help!

Hi Jessie,
A baseball diamond is in the shape of a square with the bases at the verticies. In the diagram below H is home plate, B₂ is second base, B₃ is third base and R is the position of the runner.

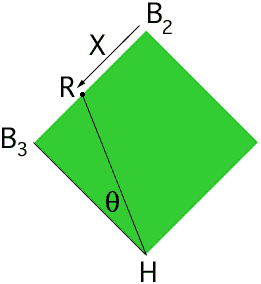
The two quantities of interest that are changing are the distance of the runner from second base, which I have called X, and the angle B₃HR which is theta. You know the rate of change of X, dX/dt = 24 feet per second and you want to find the rate of change of theta. The challenge is to find a mathematical expression that contains both X and theta.

The geomertic fact that leads to this expression is that triangle B₃HR is a right triangle. |B₃H| = 90 feet and |RB₃| = 90 - X feet, hence

If you differentiate both sides of this expression with respect to time, t, then you will have an expression that contains . If you now evaluate this expression at the time of interest, that is the time when |RB₃| = 30 feet you will have the rate of change of theta when the runner is 30 feet from 3rd base