Subject: paper cone
Date: Sat, 29 Jul 2000 14:33:29 -0400

Hi I am a grand parent 75 years old. The question of how to lay out & cut out of paper, cones came up. I would like the cone have :
A base of 4 inches
and height of
4 inches,
6 inches,
8 inches.
Thank you,
John

Suppose that you have a cone of height h, slant height s, and the radius of the base r.

 
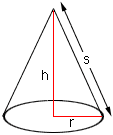
Figure 1

From the right triangle in Figure 1, s² = h² + r². Since you asked for "A base of 4 inches" I am going to assume that r = 2. Thus s is the square root of h² +2².

If you slice up the side of the cone and roll it out flat you can see the shape that is required to make the cone. It is a sector of a circle of radius s, the slant height of the cone, and arclength c, the circumference of the circular base of the cone. That is c = 2 pi r.

 
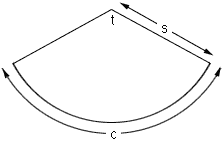
Figure 2

From Figure 2, c is an arc of a circle of radius s determined by an angle of t^o so c = (pi s t)/180, and thus t = (180 c)/(pi s) degrees.

Hence, calculate s for each of the four values of the height h using s is the square root of h² +2². Draw a circle of radius s, cut out a sector with angle (180 c)/(pi s) degrees and roll it up to form the required cone.