Hi, my name is Kay. Please help---these problems are driving me crazzzzy!!!! Your help would be greatly appreciated!

1. Let a,b be contained in R, a<b, and let f,g be continuous real-valued functions on [a,b] that are differentiable on (a,b). Prove that there exists a number c in (a,b) such that f'(c)[g(b)-g(a)] = g'(c)[f(b)-f(a)].

2. Show that f is a continuous real-valued function on the interval [a,b] and f(x)>=0 for all x in [a,b], then
   lim(int a-->b (f(x))ⁿ dx)^1/n = max {f(x):x in [a,b]}.

3. Prove that the equation cosx-x-1/2=0 has a unique real solution. Show that the fixed-point theorem is applicable to the function F(x)=cosx-1/2 and the interval [0,(pi)/4] and thereby find this solution to three decimal places.

Hi Kay,

1. When g(b) is different from g(a), you can rewrite this as
   
   which is the generalized form of the mean value theorem.

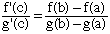
   Mean Value Theorem
   
   

   If a < b, and h is continuous on [a,b] and differentiable on (a,b), then there exists c in (a,b) such that
   

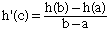
   For your problem, it is tempting to apply the mean value theorem to both f and g:
   
   

   

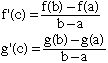
   And then divide the two equations, cancelling out the terms (b-a), but unfortunately this does not work, because the c value you get for f may not be the same as the c value you get for g. However, there is another way to use the mean value theorem to solve your problem: You apply the mean value theorem to a particular function, namely
   
   

   
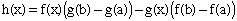
   Can you see how it works?

   P.S.
   
   

   This "generalized mean value theorem" is the key to proving that De l'Hospital's rule works: What happens if f(a) = g(a) = 0, but the limit of f'(c)/g'(c) as c approaches a exists and you are trying to evaluate the limit of f(b)/g(b) as b approaches a?
   
   
2. Let M = max {f(x):x in [a,b]}. (And suppose that M is greater than 0, otherwise the result is obvious.

   Then (int a-->b (f(x))ⁿ dx)^1/n
   <= (int a-->b Mⁿ dx)^1/n
   = (Mⁿ (b-a))^1/n = M (b-a)^1/n
   for all n.

   Therefore lim(int a-->b (f(x))ⁿ dx)^1/n
   <= lim M (b-a)^1/n = M.

   For the other inequality, you use continuity: Take B such that 0 <= B < M. Since f is continuous and reaches its maximum M at some point c, there exists an interval [u,v] containing c such that f(x) > B for all x in [u,v].

   Therefore
   (int a-->b (f(x))ⁿ dx)^1/n
   >= (int u-->v (f(x))ⁿ dx)^1/n
   >= (int u-->v Bⁿ dx)^1/n
   = B (v-u)^1/n
   for all n, whence lim (int a-->b (f(x))ⁿ dx)^1/n
   >= lim B (v-u)^1/n = B

   And since this holds for ALL B smaller than M, we have lim (int a-->b (f(x))ⁿ dx)^1/n >= M.

   P.S. For all n, |f|_n = (int a-->b (f(x))ⁿ dx)^1/n are norms on the vector space of continuous functions on [a,b], and so is
   |f|_infinity = max {f(x):x in [a,b]}.
   This exercise should help to clarify the name |f|_infinity.

3. The last part of the problem is the fun part. The theoretic limbo above just says that anyone can approximate the solution of cosx-x-1/2=0 to a high precision:

   Make sure your calculator is in RAD mode, and keep pushing the buttons

   (cos) (-) (.) (5) (=)
   (cos) (-) (.) (5) (=)
   (cos) (-) (.) (5) (=) ...

   Eventually, the numbers will start repeating. On mine, I get x = 0.41508289, and this is an approximate solution to the equation cosx-x-1/2=0.

   Now the mathematical question is "why does this work?"

   cosx-x-1/2=0 means cosx - 1/2 = x, that is x is a fixed point of the function F(x) = cosx - 1/2. By pushing the calculators buttons as above, you are just finding consecutive terms in the sequence 0, F(0), F(F(0)), F(F(F(0))), ... The (Banach) fixed point theorem says that such a sequence converges to a unique fixed point if F is a function from a complete metric space to itself which satisfies the Lipschitz condition:

   |F(b) - F(a)| <= lambda * |b - a| ,

   with lambda < 1.

   Now F([0, pi/4]) is contained in [0,pi/4] (this is important), and we can verify the Lipschitz condition using the mean value theorem: F'(x) = sinx, so that for x in [0,pi/4], we have 0 <= F'(x) <= 1/2^1/2.

   Now for a, b in [0,pi/4], there exists c between a and b such that

   F(b) - F(a) = F'(c) * (b - a),

   whence

   |F(b) - F(a)| = |F'(c)| * |b - a| <= 1/2^1/2 * |b - a|,

   and F satisfies the Lipschitz condition with lambda = 1/2^1/2.

   To find out just how much iterations you have to do before being sure that the three first decimals are correct, you need to look into the proof of the fixed point theorem.