Yesterday, I recieved a test problem asking to prove two line segments equal. Here is the problem as I was given it:

Given: paralleogram ABCD
AE is perpendicular to DB
CF is perpendicular to DB
Prove: AE is equal to CF

I answered the problem as follows:

Conclucions:	Justifications:
AB is cong. to DC	Opposite sides of a parrallelogram are congruent
AD is cong to BC	"
DB is cong to BD	Reflexive Prop of Congruence
Triangle ABD is cong to triangle CDB	SSS Triangle Congruence Theorem
AE is Equal (congruent) to CF	Congruent triangle have congruent heights (CPCF Congruence Theorem)

This problem was marked incorrect by my math teacher. I think took it to another math teacher and several classmates who all said that this was right. My math teacher refuses to help me with this. Please tell me if I have made an incorrect conclusion or if the CPCF Congruence Theorem does not apply to altitudes/heights. Thank you for your help.

Hi Erica,

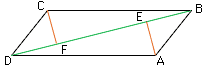
Good question. A group of us meeting at a Faculty of Education were talking about just this problem and this approach just this week. In short, I agree with you that this is a fine, insightful proof.

Perhaps it would help you teacher if you drew out a visual picture of the situation. After you have shown the congruence of ABD and CDB, show the two triangles, side by side, with the same orientation. Now it IS obvious that the two segments AE and CF are altitudes of the two congruent triangles, coming from corresponding vertices to corresponding edges.

I must admit that, as a practicing geometer, I never use such particular phrases as CPCF etc. Those should be shorthand for something that is a more basic concept. They should not be used to distract you or set aside the basic conceptual understanding and basis for the reasoning. Your approach (which others predicted to me was too sophistacted for most high school students) should be applauded.

Don't be discouraged. You are doing geometry the way I think it should be done. Unfortunately, many teachers in North America have not had a chance, themselves, to really play with geometry.

Walter Whiteley