Question: How do you find the range of the following function:

2y²/(y²+5y+6)??

I know the domain is x not equalled to -2, -3. How can one easily find the range?

Hi Michelle,

In general it is not easy to find the range of a function. Finding the domain is usually easier but even this can be difficult at times. One way to find the range, or at least make an intelligent approximation, is to use some graphing program to graph the function and read the range from the graph. I tried this with your function

I had to plot it with different scales and look at various portions of the domain, but I was able to convince myself that the range is all y greater than or equal to zero together with all y less than or egual to some number between -20 and -25. Not a very satisfactory answer.
   Another way to determine the range of a function is to find its inverse, since the range of a function is the the domain of its inverse. Usually this is quite difficult, but with your function we can do it. Consider the function

To find the inverse, interchange the roles of x and y to get

and then solve for y.

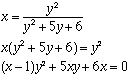
If x = 1 then y = -6/5 and if x is not 1 the general quadratic gives

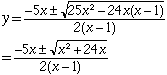
Thus we get two values for y, one with the + sign and the other with he - sign. In either case the domain, which is the range of the function you started with, is all x such that x² + 24x is greater than or equal to zero. Probably the easiest way to see which values of x make x² + 24x  0 is to sketch the graph of y = x² + 24x = x(x-24). The graph shows that x² + 24x  0 when x  -24 or x  0. Thus the range of

is all numbers which are either less than or equal to -24 or greater than or equal to 0.

Cheers,
Harley