Ashley Milliman
secondary (10-12)
I'm a student

Dealing with power of circles here. Here goes: The crankshaft of a particular automobile engine has an angular velocity of 1,500 rpm at 30 mph. The crankshaft pulley has a diameter of 10 cm, and it's attached to an air conditioner compressor pulley with a 7 cm diameter and an alternator pulley with a 5 cm diamter

At what angular velocities do the compressor and alternator turn?

The 3 pulleys are connectected my a 60 cm belt. At a crankshaft rate of 1,500 rpm, how many times will the belt revlove through it's 60 cm belt in one minute?

Most belts do not show significant wear intil each point of the belt has traveled about 20,000 kilometers. How long can the engine run at 1,500 rpm before the belt typically would wear out?

I thank you so very much for taking the time to do this. I would really appreciate it if you could breifly explain how you got the answer, so I won't need help in the future.

Thanks a lot,
Ashley Milliman

Lets look at the compressor pulley first. Put a mark on each pulley, at the top, a mark on the belt and rotate the belt until the marks on both pulleys are at the top again. Each pulley has gone through a number of complete revolutions.

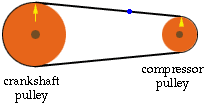
Since the diameter of the small pulley is 7 cm its circumference is 7 pi cm and the circumference of the large pulley is likewise 10 pi cm. Hence when the mark on each of the pulleys reaches the top again, the mark on the belt will have moved a distance which is a multiple of both 7 pi cm and 10 pi cm. The least common multiple of 7 and 10 is 70 and hence the marks on the pulleys will be at the top again when the mark on the belt has moved 70 pi cm.

The small pulley goes through 10 revolutions while the large pulley goes through 7 revolutions, and thus the angular velocity of the compressor pulley is 10/7 times the angilar velocity of the crankshaft pulley. That is the angular velocity of the compressor pulley is 10/7(15,000) = 21,429 rpm.

I hope this helps,
Harley