Subject: calculus problems

Hello, i'm a teacher in Dallas, Texas and a student asked me to help her with these problems and I'm stuck. Any help you could give would be great.

Thanks

Question #1

Assume that a snowball melts so that its volume decreases at a rate proportional to its surface area. If it takes three hours for the snowball to decrease to half its original volume, how much longer will it take for the snowball to melt completely? It's under the chain rule section of differentiation if that any help.

I've set up a ratio and tried to find the constant but am stuck.

Question #2 The figure shows a lamp located three units to the right of the y-axis and a shadow created by the elliptical region x^2 + 4y^2 < or= 5. If the point (-5,0) is on the edge of the shadow, how far above the x axis is the lamp located?

The picture shows an x and y axis with only the points -5 and 3 written on the x axis. the lamp is on the upper right quadrant shining down diagonally to the left. There's an ellipse around the origin creating the shadow. It's formula is given as x^2 + 4y^2=5.

Any help would be great.

Hi

For the first problem the volume of a sphere is

V = 4/3 pi r3

and the surfave are is

A = 4 pi r2

V, A, and r are all functions of time, t. You are also told that

where k is a constant. Using the chain rule

and observing that

you get

Hence the radius is decreasing at a constant rate. Now write V(t) and r(t) for the volume and radius as functions of time then you know that V(3) is one half of V(0) and thus

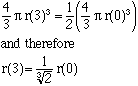
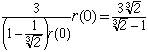Thus the radius decreases units in 3 hours and therefore it decreases r(0) units, that is decreases to zero, in minutes.

For the second problem I have the diagram

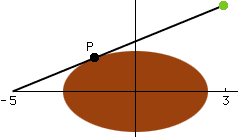
The crutial point here is that the line from the light to the point (-5,0) is tangent to the ellipse at the point I have called P. What you need to do is find P, write the equation, y = mx + b, of the tangent line and then substitute x = 3 to find the height of the light.
   Let the point P have first coordinate a then its second coordinate is (take the positive square root since the second coordinate is clearly positive). Either solve the equation of the ellipse and differentiate or differentiate implicitly to find that the slope of the tangent line at P is . Since the tangent line passes through (-5,0) and P you can also find the slope using the "rise-over-the-run" expression. This leads to

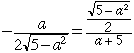
Solving for a gives a = -1. Now substitute a = -1 into the expression for the slope, write the equation of the tangent line and substitute x = 3.

Cheers,
Harley

Go to Math Central