Hi my name is Kevin Palmer and my calculus teacher recently gave us a week to work on this extra credit problem. I have no idea where to even start to find the answer. If you all could help, it would be greatly appreciated. Thanks! Here is is:

With the Olympics fast approaching the networks are focusing in ona new and exciting runner from Greece. Thearcius Functionius has astounded the world with his speed. He has already established new world records in the 100 meter dash and looks to improve on those times at the 2000 Summer Olympics.

Thearcius Functionius stands a full 2 meters tall and the networks plan on placing a camera on the ground at some location after the finish line(in his lane) to film the history making run. The camera is set to film him from his knees(0.5 meters up from the ground) to 0.5 meters above his head at the instant he finishes the race. This is a total distance of two meters(the distance shown by the camera's lens).

0. Write an equation for the lens angle(y) in terms of the distance(x) the camera is from the finish line.
    
   
1. Find dy/dx in terms of x.
    
   
2. At what distance from the finish line should the camera be placed so that the camera lens angle is a maximum

I would start by drawing a diagram.

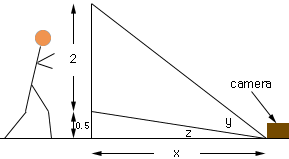
From the diagram tan(z) = 0.5/x and tan(y + z) = 2.5/x. But the lens angle y can be written y = (y + z) - z and thus tan(y) = tan[(y + z) - z]. Now use a trig identity to write tan[(y + z) - z] in terms of tan(y + z) and tan(z) and thus find a relationship between y and x.