Joshua D. Parham
Calculus Student
Dade County High School
Trenton, GA

The problem that I am not able to solve is this:

If n is a positive integer, then

lim	(1/n)[1/(1+1/n) + 1/(1+(2/n) + ... + 1/(1+n/n)]
n->infinity

can be expressed as the integral from 1 to 2 of 1/x dx

Question how did they get this solution??? Thanks in advance for your help

The relationship you are looking for comes from expressing the integral in terms of Riemann sums. Specifically divide the interval from 1 to 2 into n subintervals of equal lengths and then construct rectangles as in the diagram.

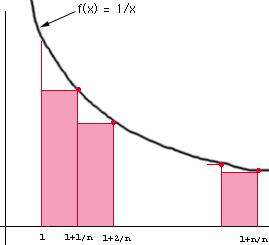
The integral is obtained by adding the areas of the rectangles and then taking a limit as n approaches infinity. For example the rectangle on the left has a base of length (1 + 1/n - 1) = 1/n and height f(1+1/n) = 1/(1+1/n), and hence its area is (1/n)(1/(1+1/n)). If you continue and write the area of each of the rectangles, sum them and take the limit as n approaches infinity you will obtain the expression in your problem.