Question: The question I have to answer is: Find the rate of change of the distance between the origin and a moving point on the graph of y=sinx if dx/dt=2 centimeters per second.

So far I have:
(d/dt)[y]=(d/dt)[sinx]
(dy/dt)=(dx/dt)[cosx]
(dy/dt)=2[cosx]

I know my answer is wrong because the answer should have no variable (like x) left in the equation. I must have messed up on the implicit differentiation. Any help on this problem would be greatly appreciated. Also, please don't just give me the answer, I would like to know the steps I should take to get the correct answer so I won't have any problems if an answer similar to this should appear on the chapter test.

Below is the graph of y = sin(x) with the point P which is moving along it. P has coordinates (x, sin(x)).

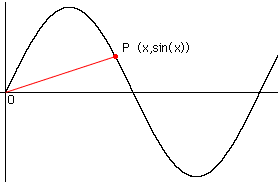
The distance from the origin to the point is the length of the line segment OP so the distance is given by

The rate of change of this distance is dy/dt, with dx/dt = 2 cm/sec.

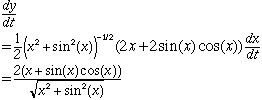
The fact that the variable x appears in the answer is quite natural. The rate of change of the distance from the origin to the point depends on the position of the point P, and you were not given the position. If the question had asked "Find the rate of change of the distance between the origin and a moving point on the graph of y=sinx if dx/dt=2 centimeters per second and x = pi/4." you would then substitute x = pi/4 to get a numeric answer.