Sender: "Sanker"

Sir.,

I need help to solve this Rules for bulding towers of cubes
rule 1 The number of cubes on the bottom layer is always one less than the number of squares on the grid
rule 2 Each new layer is made with one cube less than the layer underneath it.

  1. Investigate how many different arrangements there are of 4 cubes on top of 5 cubes on a two by three grid

  2. investigate the number of different arrangements of six cubes on top of seven cubes on a two by four grid

  3. investigate the relation between the number of arrangements of cubes and the size of the grid
    • when there are two layers of cubes
    • when there are more than two layers of cubes
Maths" grade 11

Hi Sanker,

I would approach this problem visually. Actually with two images:

The first image:
(a)For the first layer, I would imagine the grid and the blocks placed.
How many ways are there to place 5 blocks on six squares?
Alternately, how many ways are there to pick the square with no block on it!
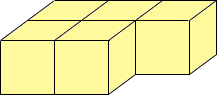(b)Now imagine the five blocks placed in some patttern. How many ways are there to pick the four blocks to place a block on top of?
Alternately, how many ways are there to pick the one block that will not have a new block on top?
[Check that this number does NOT depend on which five squares were covered in the first layer!]
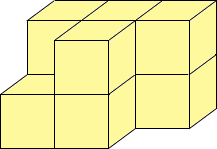(c)Proceed to the next layer (if there are more than two layers) in the same way.
The second image is a basic counting principle. You have layers (in a specific order). I think of them (for this problem) as a vertical stack of rectangles. In each rectangle, I place the corresponding number from above. The principle is that these numbers should be multiplied, because EACH possibility counted at a lower layer had ALL the possibilities counted in the upper layer.

Therefore you multiple your answers to (a) x (b) [ x(c) if you have more layers].

I think you can figure it out from here. If you are stuck , image a 2x2 grid:
(a)How many ways to choose three? (Think of it as choosing one to omit.)

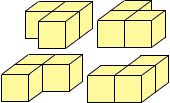There are 4 ways.
(b)For each of these, how many ways are there to pick two of these to cover? (Or one to not cover) For each of the 4 options above there are 3 ways to pick two to cover. For example for the first of the 4 options above the three ways are.

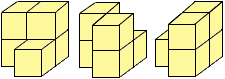
Hence in total there are 4 x 3 = 12 towers.

Cheers.
Walter

Go to Math Central