My question has to do with the length of a diagonal. This problem came up when I thought about the shortest distance between two points, for example walking from one point to another in my neighborhood. I can choose a zig zag route and assuming the blocks I walk are exactly the same length, it shouldn't matter what route I took, the distance I travel should still be the same when I reached my goal. If, on the other hand I could travel in a diagonal line, the distance would be shorter. So, question one, am I right to assume the diagonal will be shorter than the two sides added together?
In a square, if I start at one corner and travel along two sides to get to the opposite corner, the length of two sides equals one value. The diagonal from one corner to another corner equals a different value. What if I divide the sides of the square into sections that are much smaller. Added together, no matter how many sections I ultimately have, they should end up equaling the length of my two orginal sides. But what if, in my zig zag motion, the sections get so small the route aproaches a diagonal. Shouldn't it be that each separate section added together equals the value of the two original sides? Or would it suddenly equal the value of the diagonal (which, of course was shorter than the two sides added together)?
What gives?
Hi Dagmara,
What a nice observation! You have taken the first step toward discovering fractals. You are correct in your assumption that the diagonal will be shorter than the two sides added together. By extending your zig-zag path argument you can easily construct a path from A to B whose points are as close as you wish to the line AB (say, within a distance of 10-100), with the length of the zig-zag as long as you wish.
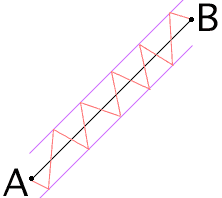
Studying the length of a curve is usually postponed to the end of an introductory calculus course. It is more difficult than other concepts you study in calculus, like areas for example. As you have observed, estimating the length of a "curve", even when the curve is a straight line, is a delicate operation. If you have a "smooth" curve (not too many sharp corners) you can estimate its length by selecting some points on the curve, joining them by straight line segments and then adding the lengths of the line segments.

If you want a better estimate of the length of the curve add a new point between each pair of points you already have.
Thanks for the great question,
Chris and Harley