2 questions:
- find the product of all the divisors of 2000
- dog trainer time has 100m of fencing to enclose a rectangular exercise yard. One side of the yard can include all or part of one side of his building. iff the side of his building is 30 m, determine the maximum area he can enclose
can you please show how you did it as well
Thank you
Amanda Semi
age17
Hi Amanda,-
You can pair off the divisors of 2000 in pairs of divisors whose product is 2000: {1, 2000}, {2, 1000}, {4, 500}, ..., {500,4}, {1000,2}, {2000,1} in general, you pair off a with 2000/a. This is always a different divisor because 2000 is not a square, so it has no divisor a such that a = 2000/a.
The product of the two members of a pair is always 2000. Notice that in the list of pairs above there are as many pairs as there are divisors of 2000. However each divisor appears twice in the list so the product of ALL the divisors of 2000 is 2000 to the power of half the number of divisors of 2000. So, all you need to do is find out how many divisors 2000 has. Do you know how to do that?
The extension of this fact to say that "the product of ALL the divisors of N is N to the power of half the number of divisors of N" is valid even if N is a square. To illustrate let N = 225 = 152. Suppose that N has k divisors and M is the product of the k divisors of 225. Write the k divisors of M in two ways, first as a list in increasing order and then as a list in decreasing order. That is:
1 3 9 ... 25 75 225 225 75 25 ... 9 3 1 The product of the numbers in each of the lists is M. Multiply both lists together by multiplying down first and then across. That is:
M*M = (1*225)*(3*75)*(9*25)*...*(25*9)*(75*3)*(225*1)
= 225*225*225...*225*225*225
= 225kHence
M2 = 225k and thus
M = 225k/2
-
This is like using fencing to enclose a rectangular area alongside a river. The difference is that the building has a short length (30 meters), while the river would certainly be longer than the side of the enclosure.
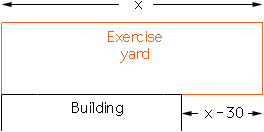
The first part of the solution consists in supposing that the building will be long enough, so you disregard the constraint that it is just 30 meters. This is a temporary hypothesis that allows you to treat the problem like the "fencing alongside the river" problem: Let x be the length (in meters) of the sides of the enclosure that are parallel to the building. Then 100 - x meters are left for the sides that are perpendicular to the building (because we suppose that the building is long enough), so these sides have to be (100 - x)/2 meters each. Then the area of the enclosure is A(x) = x * (100 - x)/2 m^2, and you find the maximum of this area using calculus.
There are then two possibilities:
1) The x value that maximizes the area is at most 30. This justifies your hypothesis that the building will be long enough, thus you have already found the solution.

2) The x value that maximizes the area is more than 30. This means that your solution is not accurate because the side that is partly bordered by the building is left open. This means that you have to start over, but at least you know that in your solution, the sides parallel to the building will be more than 30 meters. Let x be the length (in meters) of the sides of the enclosure that are parallel to the building. Then x > 30, and in all, x + (x - 30) = 2x - 30 meters of fencing are used on these sides. Thus 100 - (2x - 30) = 130 - 2x meters of fencing are left for the other sides, so these are (130 - 2x)/2 meters each. Your area function is thus A(x) = x * (130 - 2x)/2. All you need to do is find its maximum.
 Cheers,
Cheers,
Claude