Name: Kaushal Shah
Who is asking: Student
Level: Secondary

Question:
How do I Calculate the area of a ellipse known the length of any related thing. Example, suppose if I know the length of latus rectum, major&minor axis etc.

There is a simply way to make sense out of the area of the ellipse.

We can see the ellipse with major axis of length 2A and a minor axis of length 2B as a stretched (along A) version of the circle of radius B.

If you slice, parallel to the major axis, then each slice of the ellipse is bigger than the corresponding slice of the circle, in a Ratio of A/B. This consistent change of all the slices means a consistent change in the area. (In the diagram K is the square root of B² - X².)

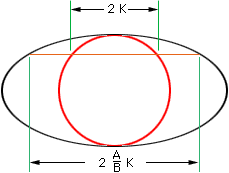
The area of the ellipse is then

The circle then reappears as the special case when A=B.

This kind of comparison of slices argument for area is very ancient. It was used by the Greeks for areas and volumes. It is really the kind of argument at the heart of Area by Integration (when you get to Calculus).