Question Level: secondary (10)
Who is asking the question: father (for his daughter)
How is the following problem solved? It's an extra credit problem and my daughter's teacher has encouraged her students to go to their parents, etc. in learning how to solve it.
You have two candles the same length. They are lit at the same time. One burns down in 4 hours; the other in 5 hours. How long does it take before one candle is three times the length of the other candle?
Hi Skip.
First a picture so you know what to expect (from any formulae etc.)
They start at equal lengths. After four hours one has length 1/5, the other
length 0. So the RATIO of the two candles is running from 1 to infinity,
continuously. Sometime in between the ratio is 3.
Now, there is a graph which will give the answer, or a formula which gives the answer. Try the graph first.
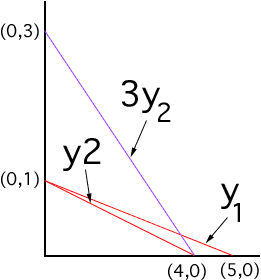 |
On the graph put time along the bottom and height along the y axis.
The actual height does not matter -just the ratios. Pick the initial
height as 1, just to get started. Now the first candle has height running from 1 at time 0 to 0 at time 5 hours. With those two points draw the first line, labeled y1. The second candle has height 1 at time 0 and 0 at time 4 hrs. That give the second line, y2. You want to know for which time t, the point on the first line is 3 times the height on the second line. On the picture you can just take the second line, multiply it by 3, (i.e. run it from height 3 at time 0 to height 0 at time 4 hrs) and see where it crosses the first line. That point is where the original heights had a ratio of 3 to 1. If, by chance, you are used to using software like geometer's sketchpad, you could make a nice animated image and check for various ratios. As a novice, you may need to 'see' this drawn out. The only difference for an expert is that I can make this picture and 'see' what will happen in my mind's eye! |
With algebra, you can write y1= m1 t + b1 for the first line finding m1 and b1 from the points.
Similarly you can write y2 = m2 t + b2 for the second line, from its points.
You want to find the time t when y1 = 3 y2 or m1 t + b1 = 3(m2 t + b2) I trust you can take it from there.
Of course, given a proposed answer, you can check it! In fact, however you get the answer, you should check it!
Walter Whiteley