Hi,

For the case of 3 Trolls and 3 Gargoyles you can count the number of seatings without too much difficulty. Even in the 4 and 5 case you can count the number of seatings. For the general situation I don't know a simple formula.
   For the 3 Trolls and 3 Gargoyles situation it is helpful to distinguish three cases; there are 3 Trolls in a row, there 2 Trolls in a row but not 3 and no Troll sits beside another Troll.
   In the first case there is only one arrangement.

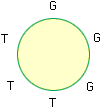
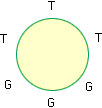
In these "circular permutation" problems the usual interpretation is that the initial positions at the table are indistinguishable so, in particular, the above arrangement is indistinguishable from

   If there 2 Trolls in a row but not 3 then there are two possible arrangements

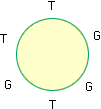
and

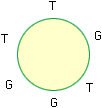
   If no Troll sits beside another Troll there is only one seating arrangement, alternate the Trolls and Gargoyles. Thus there are a total of 4 ways can you seat 6 monsters.

Cheers,
Penny