Date: Fri, 28 Jul 2000 23:55:19 EDT
Subject: geometry question

I am not a student. A smart ass friend of mine posed this question to me as a challenge and for the life of me, I can't remember how to do it.

I assume this is a high school level question. I am an adult (25).

Here is the question:
An equalateral triangle is enclosed in a circle. The three corners touch the edges of the circle. One side of the triangle is 12. What is the circumference of the circle?

Join each vertex of the triangle to the center of the circle to form three, congruent isosceles triangles. Condider one of these tringles, the one I have shaded green in the diagram.

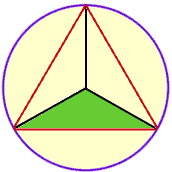
The angle in this triangle at the center of the circle has measure 360^o/3 = 120^o. The sum of the angles in any triangle is 180^o hence each of the other angles in this triangle has measure (180^o - 120^o)/2 = 30^o.

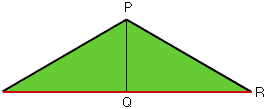
Drop a perpendicular from the vertex of this triangle (center of the circle) to the side of length 12 to form a triangle PQR. |QR| = 12/2 = 6, angle QRP is 30^o and RP is the radius of the circle. You should now be able to find |RP| and then calculate the circumference of the circle.