Hello,

Long-time ago I red an article about surprizing (and in a way frustrating) results in math, for example the limit of a nicely defined infinite series which was believed to beÊa simple rational number, but laterÊwas determinedÊto be a transcendent number thatÊmissed the rational value by an incredibly small amount (so for example the limit proved to be 2.75000...00137.. with a lot of 0's in between). I cannot find that article anymore, so i was wondering if you have any such examples, or you can point to any relevant information source?

Thanks a lot,
Adrian Valc.

Hi Adrian,

The article you saw was probably J.M. Borwein & P.B. Borwein, Strange Series and High Precision Fraud, The American Mathematical Monthly, Volume 99, Number 7, (Aug-Sep 1992) 622--640. Some of the results are listed below.

1. Let a(n) count the number of odd digits in odd places in the decimal expansion of n. (a(901) = 2, a(210) = 0, a(811) = 1, here the first digit is the first digit to the left of the decimal point.) Approximation correct to 99 digits.

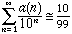
2. Let c(n) = 32c₁(n) - c₂(n)/32 where c₁(n) counts the number of nines in n and c₂(n) counts the number of eights in n(c(8199) = 32*2 - 1/32). Approximation correct to 240 digits.

3.   Approximation correct to at least 18,000 digits.

4.   Approximation correct to at least 42 billion digits.

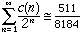
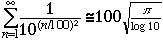
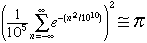
Cheers,
Chris