Name: Wallace
level: secondary
Who: student

Thankyou for responding to my previous question with such clarity and celerity. Here is another question:

Consider the points 1, 1/2, 1/3, ... on the real number line. You are given five small bars, all of length p, which are to be placed on the number line such that all points will be covered. What is the minimum value of p that will allow you to do this?

Once again, I am grateful for your help. Thank you.

I made a diagram and tried rods of length 1/6.

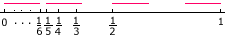
Since the numbers 1, 1/2, 1/3,... approach 0 one of the intervals must start at 0, and thus extends to 1/6. The second bar can then start at 1/5 and extends to 1/5 + 1/6 = 11/30 which is larger than 10/30 = 1/3. Hence all that remains is 1/2 and 1 and two more rods will suffice. Thus if p = 1/6, 4 rods will cover the points.

If you try rods of length 1/7 then the first one extends from 0 to 1/7 and the second can start at 1/6. 1/6 + 1/7 = 13/42 which is larger than 1/4 but smaller than 1/3. Thus the second bar covers 1/6, 1/5 and 1/4. Thus the third bar can start at 1/3 and extends to 1/3 +1/7 = 10/21 which is less than 1/2. Thus two more bars are required, one to cover 1/2 and one to cover 1.

Continuing in this fashion you will see that 5 rods of length 1/10 can cover the points but 5 rods of length 1/11 can not. In fact if you try with rods with length which is less than 1/10 and larger than 1/11 then the first rod extends from 0 beyond 1/11 but not to 1/10. Thus the second rod must start at 1/10 and extends less than 1/10 + 1/10 = 1/5. Hence the third rod must start at 1/5 and extends to less than 1/5 + 1/10 = 3/10 which is less than 1/3. Thus you need a fourth rod to cover 1/3, a fifth rod to cover 1/2 and a sixth to cover 1. Therefore the minimum that p can be is 1/10.