Name: alex waller
Who is asking: Parent
Level: Middle

Question:
What are some practical applications for absolute value?

Hi Alex,

I can give you two related but different applications of absolute value. The first comes from "Discovering an Optimal Property of the Median", pages 692 to 703 in the November 1999 issue of Mathematics Teacher, a publication of The National Council of Teachers of Mathematics. The second paragraph of this article is:

For example, a gasoline company would like to determine the location of a distribution center for its gasoline trucks. Suppose that n stations must be serviced along a highway and that the trucks can carry only enough gasoline for one station at a time. Since the cost of transporting gasoline from the center to the various stations is quite expensive and is proportional to the distance travelled, the company would like to select a location that minimizes the total distance, that is the sum of the absolute values of the distances of the stations to the distribution center, that the gasoline must be transported. Suppose for example that there are n = 5 stations along the road at miles 3, 5, 6, 14 and 21.
 

 
If the distribution center is to be at mile D then the total absolute distance is given by
 
f(D) = |D-3| + |D-5| + |D-6| + |D-14| + |D-21|

 
To determine what value of D minimizes f(D) you can plot the graph of f(D). You can do this with a graphing calculator or by hand.


 
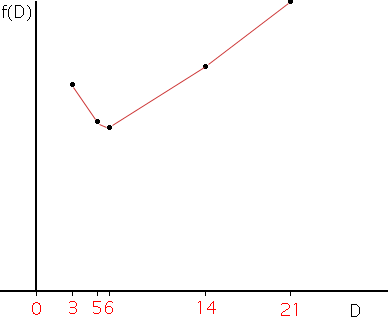
The graph shows that F(D) is a minimum when D = 6 miles. It is interesting to eliminate one of the stations so there are only 4 (an even number) and go through the exercise again to see where the distribution center should be located.
   The second application is from statistics. When given a data set statisticians quite often want to answer two questions. Where is the "center" of the data and how "varied" is the data set? The most common measure of the center is the average (statisticians call it the mean) but another measure used is the median. To find the median order the data from smallest to largest and then the median is the middle observation. If there is an even number of observations then the median is any number between the middle two.
   Once you decide on the center you can measure the variability or dispersion by asking "What is the average distance from the individual observations to the center?" If the center is the median then this quantity is called the mean deviation. For the data set in the distribution center example above, 3, 5, 6, 14, 21 suppose the center is the median, 6. The mean deviation is then
 
(|6-3| + |6-5| + |6-6| + |6-14| + |6-21|)/5 = 27/5 = 5.4

 
Cheers,
Harley 		 

Go to Math Central