Name: Sheryl Webb
Who is asking: Teacher
Level: Secondary

Question:
I am trying to find a proof of the theorem: Given n points in a plane, there is a line that contains exactly two points.

There are hundreds of books and papers that would provide a proof. The result is referred to as Sylvester's Problem. Two proofs are given in Introduction to Geometry by HSM Coxeter, pages 65-66 and 181-182. Below is the proof that appears on pages 65 and 66 which Coxeter attributes to L. M. Kelley. This proof uses the concept of distance in Euclidean space where the proof on pages 181-182 uses only ordered geometry.

If n points in the real plane are not on one straight line, then there exists a straight line containing exactly two of the points.

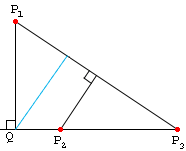
The n points P₁,...,P_n are joined by at most 1/2 n(n-1) lines P₁P₂, P₁P₃, etc. Consider the pairs P_i, P_jP_k, consisting of a point and a joining line which are not incident. Since there are at most 1/2 n(n-1)(n-2) such pairs, there must be at least one, say P₁, P₂P₃, for which the distance P₁Q from the point to the line is the smallest such distance that occurs.

Then the line P₂P₃ contains no other point of the set. For if it contained P₄, at least two of the points P₂, P₃, P₄ would lie on one side of the perpendicular P₁Q (or possibly one of the P's would coincide with Q). Let the point be so named that these two points are P₂, P₃, with P₂ nearer to Q (or coincident with Q). Then P₂, P₃P₁ is another pair having a smaller distance than P₁Q, which is absurd.

Cheers,
Chris