Subject: Surface area of a sphere

How can I demonstrate to my middle school students the reason for the formula for the surface area of a sphere?

Thanks!
Gina

A connection which could be illustrated, and could be understood by students who know the perimiter of a circle, runs as follows:

Put the sphere of radius R inside a cyclinder, with the cylinder just touching the equator, and cut off at the height of the top and bottom of the sphere. (A cutaway veiw is in the diagram.)

What is the area of the curved part of the cylinder? 2 Pi R x 2R = 4 Pi R². This is found by slicing the cyclinder surface and rolling it out as a rectangle.

Now, it is NOT an accident that the cylinder surface is EXACTLY the area of the sphere.

Take in small horizontal slice through the diagram. (I have coloured one such slice orange.) This cuts a rectange out of the rolled out cylinder and slightly distorted rectangle out of the sphere. (If the slice is very thin then the distortion is "slight".)

In the cross-sectional view below h_c is the height of the slice on the cylinder, h_s is the length of the arc on the sphere cut out by the slice, r is the radius of the distorted rectangle on the sphere and R is the sadius of the sphere.

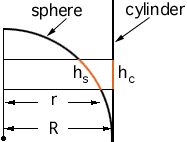
The area of the orange rectangle on the cylinder is 2 Pi R h_c and the area of the distorted orange rectangle on the sphere is approximately 2 Pi r h_s. These two areas are approximately equal (the proof is outlined below). Since the cylinder and the sphere can be decomposed into these recangular strips, the area of the sphere and the area of the cylinder are approximately equal.

This argument is in the spirit of how the greeks compared slices to show that areas and volumes are the same. It is not only interesting reasoning in proportion, etc., but it is a lesson in History.

In the same spirit, you can compare the VOLUME of a hemi-sphere with that of the cyliner with an inverted cone removed. (I think of the hemisphere with the equator at the bottom and the cone with the 'base' at the top). Now, for each horizontal slice, the area of the slice of the sphere (a circle) is exactly the area of the cylinder outside the cone. SInce all slices have the same area, the volumes are equal.

Volume of hemisphere = Pi R² x R - (1/3) Pi R² x R = (2/3) \Pi R³. Again, this is the way the volume was computed by the Greeks.

Walter and Chris

In the diagram below K is the center of the sphere. Construct a tangent line PA to the sphere at P and drop a perpendicular from A to meet QP at B. Since PA is tangent to the sphere, angle KPA is a right angle.

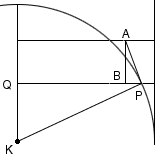
Since triangle KPQ is a right angle triangle, angle QKP + angle KPQ = 90^o. But angle KPQ + angle BPA = 90^o, and thus angle QKP = angle BPA. Hence the right triangles QKP and BPA are similar. Thus PQ:KP = AB:PA. But |PQ| = r, |KP| = R, |AB| = h_c and |PA| is approximately h_s and thus R h_c is approximately r h_s. Thus the area of the orange rectangle on the cylinder, 2 Pi R h_c and the area of the distorted orange rectangle on the sphere 2 Pi r h_s are approximately equal.