Subject: question on trig

Name: will
Who is asking: Student
Level: Secondary

Question:
An open rectangular tank a units deep and b units wide holds water and is tilted so that the base BC makes an angle theta with the horizontal. When BC is returned to the horizontal, who that the depth of the water is

(a squared) * cot theta div 2b units

Was there a diadram that went with this problem? I ask because your statement is true in some situations but not in others.

Suppose the diagram is as below.

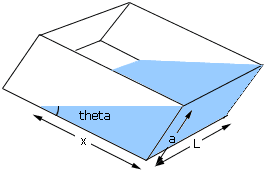
The volume of water in the tank is the area of the triangular face times the length of the talk, L. If the base is returned to horizontal then the volume is the area of the rectangular face, b*d, times the length, L.

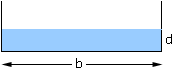
Since the volume of water is unchanged the area of the triangular face in the first diagram must be b*d. But the area of the traiangle is x*a/2 = a²/2*cot theta and thus b*d = a²/2*cot theta. Thus d = (a²cot theta)/(2*b).

Now suppose that a = b and the front face of the the original diagram looks like the diagram below, with cot theta > 2.

In this case your expression d = (a²cot theta)/(2*b) gives a depth of d = (a²cot theta)/(2*a) > a, which is impossible.