Name: Mr William
Who is asking: Student
Level: Secondary

Question:
Prove that root 3 is irrational
Thanks

I have taken a proof from the notes for a course I teach. The proof is that root 2 is irrational but that should illustrate the procedure. We use what is called a proof by contradiction. The essential idea is that we make an assumption and if we follow that up with a number of logical steps and end up with a false statement, it must be that our assumption was false.

So, let's assume that 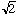is rational, in particular assume that 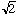= ^p/_q where p and q are relatively prime integers. Thus,

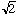• = ^p/_q, and hence (squaring both sides)
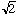• ()² = (^p/_q)² .

Equivalently,

• 2q² = p².

Here's where we use our number theory sense (on divisibility properties) -- we know 2 | 2q², thus 2 | p². But this means that p² must be even. The only way this can happen is that p itself is even. For simplicity's sake let's write p = 2m. Then we have

• 2q² = p² = 4m², and
• q² = 2m².

But now 2 | 2m² leading to 2 | q². The only way this can happen is that q is even also! But then we have both p and q being even when we've already assumed that they were relatively prime. This can't be.

Thus, something has gone wrong! What? It can only be our assumption that 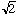= ^p/_q where p and q are relatively prime integers. 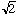cannot be rational and must be irrational.