Hi,

My name is Will. Level: (10-12)

I have been having some problem with the following question for some time. I would appreciate any help on solving the problem or a solution.

Q: Assume that a system of equations in the unknowns x1, x2, x3, x4 and x5 when converted to row echelon form gives

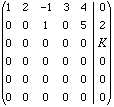
Solve, if possible for x1, x2, x3, x4 and x5 in the two cases

(a) k = -3
(b) k = 0.

Please help. Thanks.

If k = -3 then the third row of your matrix represents the equation

This is clearly impossible and thus if k = -3 then the system of equations has no solution.

If k = 0 however the system has infinitely many solutions. To describe these solutions I would first put the matrix in reduced row echelon form by adding the second row to the first row to get

The two remaining, non-zero rows represent the equations

This gives infinitely many solutions since you are free to assign arbitrary values to x₃, x₄ and x₅ and then compute values for x₁ and x₃ to form a solution.