Subject: Calculus Research Questions

I am a Calculus Teacher, and me and my class ran into these two problems without solutions in my manual, we got answers, but are unable to check them. If anyone gets this email and can respond to this with the solutions it be greatly appreciated.

Thanks,
William Wright

1. f(x) = intergral from 0 to x³ of (t³ - t)dt then f"(1) = ?
    
   
2. Let f and g be continuous functions with the following properties:
   • g(x) = A - f(x), where A is a constant
   • integral from 1 to 2 of f(x)dx = integral from 2 to 3 of g(x)dx
   • integral from 2 to 3 of f(x)dx = -3A
      
     
   a) Find the integral from 1 to 3 of f(x)dx in terms of A
   b) Find the average value of g(x) in terms of A over the interval [1,3]
   c) Find the value of k if the integral from 0 to 1 of f(x + 1)dx = kA

Problem 1 can be done in two ways. First you could integrate and then differentiate twice.

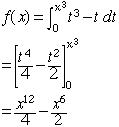
Then

The second method to solve this problem is to use the second form of the Fundamental Theorem of Calculus which says that

For your problem the upper limit in the integration is x³ so you need to use the chain rule when you differentiate. Hence

Now you can differentiate once more and evaluate at x = 1.

Problem 2

Part a)

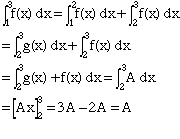
Part b)

The average of g(x) on [1,3] is

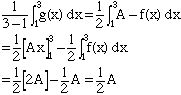
Part c)

Make the change of variables u = x + 1 then du = dx. When x = 0, u = 1 and when x = 1, u = 2. Thus

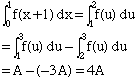
Hence k = 4.