My name is Steven, I am 11 years old and in grade 6 at Caronport Elementary School. In math we were finding the number of diagonals in a polygon. I was wondering if there was a shortcut. I fooled around with it and came up with a formula - the number of diagonals in a polygon with n sides is
d = 2(n-3) + (n-4) + (n-5) + ... + 3 + 2 + 1.
Is there a way to improve this formula such as writing it in a shorter form?
Thank you for your interesting question. Your formula d = 2(n-3) + (n-4) + ... + 2 + 1 for the number of diagonals of an n-sided polygon is indeed correct. There are a number of ways to get this.
Think of the n points on your polygon as n people standing in a circle (at this stage there are no lines drawn). We draw a line between two people when they shake hands. If everyone shakes hands what you want to count is the resulting diagonal lines, that is, count all the lines except the n lines formed as the outside edges of the polygon.
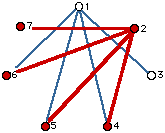
First, let's get your formula then I'll show you another way to get the same answer (even if it looks different). Call the people by the names 1, 2, 3, ..., n. Let person #1 shake everyone's hand except the 2 people beside him (this corresponds to the diagonal lines from person #1). This accounts for (n-3) handshakes - there are n people, #1 doesn't shake his own hand or #n's or #2's. If person #2 does the same thing she would also shake n-3 hands (not her own and not #1 or #3). Now it gets a bit tricky. If we do the same with #3 we only count (n-4) handshakes this time as #3 has already shaken hands with #1 and we don't want to count it again! If we then do the same with #4 we only count (n-5) handshakes this time as they have already shaken hands with #1 and #2 and we don't want to count them again! If we do the same with #5 we only count (n-6) handshakes this time as they have already shaken hands with #1 and #2 and #3 and we don't want to count them again. And so on. See the pattern? Just to make sure let's look at a few of pictures when n = 7.


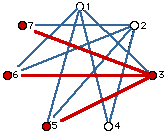
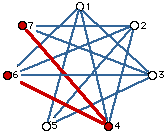
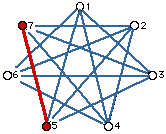
All told we have 4 + 4 + 3 + 2 + 1 = 14 handshakes (diagonals). In general you get
d = (n-3) + (n-3) + (n-4) + (n-5) + ... + 3 + 2 + 1, as you came up with.
Have a look at d for different values of n.
If n = 3, d = 0. If n = 4, d = 2. If n = 5, d = 5. If n = 6, d = 9.
If n = 7, d = 14. If n = 8, d = 20. If n = 9, d = 27. If n = 10, d = 35.
I'll bet you might spot some other patterns here! Notice how d goes up from one value of n to the next. Can you now predict d for n = 11 from the answer for n = 10?
If one spends time with your formula you can show, with a fair amount of effort, that d in fact satisfies d = n(n-3)/2. For example, if n = 7, d = 7 (7-3)/2 = 28/2 = 14. It usually takes math you learn in grade 10 or 11 to do that unfortunately. So, that's no good for us; can we possibly show d = n(n-3)/2 is right by some other means?
Look at the picture with n = 7 above. Notice that each person has 4 lines (handshakes). Thus if we count handshakes for each person we get a total of 7(4) = 28 lines (diagonals), but, AND THIS IS A VERY BIG BUT, notice if we do that each handshake is counted twice - once by each person involved in the particular handshake. This means we really don't have 28 lines but one half of that amount, namely 14. In general with n people each is joined to (n-3) others making n(n-3) lines in all BUT we've counted each line twice again so we have to take half of that for a total of d = n(n-3)/2.
Good luck with your math! Write us again if you have more questions.
To return to the previous page use your browser's back button.